स्थिर आणि अनिश्चित एकीकृत दरम्यान फरक
कॅलकुल्स गणिताची एक महत्त्वाची शाखा आहे आणि कलनशास्त्रामध्ये फरक एक महत्वपूर्ण भूमिका बजावतो. भेदणाची उलटा प्रक्रिया एकात्मता म्हणून ओळखली जाते, आणि व्युत्पन्न अभिन्न म्हणून ओळखली जातात, किंवा फक्त ठेवली जातात, फरकच्या व्यस्तांना एक अविभाज्य प्रदान करते. त्यांनी ज्या परिणामांचा आधार घेतला त्या आधारावर ते दोन वर्गांमध्ये विभागले जातात उदा., निश्चित आणि अनिश्चित अनंत
निश्चित एकात्मिक
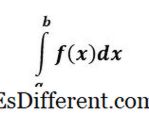
f (x) एक निश्चित अभिन्न अंग आहे आणि वक्र < f (x) पासून x = a ते x = ब < एक निश्चित अभिन्न भाषेच्या वरच्या आणि खालच्या मर्यादा आहेत, आणि त्यास निश्चित म्हटले आहे कारण, समस्येच्या शेवटी, आपल्याजवळ एक संख्या आहे - हे एक निश्चित उत्तर आहे.
अनिश्चित इंटिग्रल < च (एक्स) चे अनिश्चित इंटीग्रल एक फंक्शन आहे आणि प्रश्नाचे उत्तर आहे, "विभेदित केल्यावर कोणते कार्य
f (x)देते? "

एक अविश्वनीय इंटीग्रल सह इथे अविभाज्य अशी कोणतीही वरची व खालची मर्यादा नाही, आणि आपल्याला काय मिळेल ते एक उत्तर आहे जे अजूनही x आहे आणि त्यात एक स्थिर सामान्यत: < C < द्वारे दर्शविले जाते).
F (x) = ∫ƒ (x) dx
किंवा
F = ∫ƒ dx < असे लिहिले आहे जिथे F आणि ƒ < < x चे कार्य आहेत आणि
F
वेगळा आहे. वरील स्वरूपात, याला रेमॅन इंटिग्रल असे म्हणतात आणि परिणामी फंक्शन एका अनियंत्रित स्थिरतेसह असतो.
एक अनिश्चित इंटिग्रल बहुतेक वेळा फॅक्ट्रीचे एक कुटुंब उत्पन्न करते; म्हणून अविभाज्य अनिश्चित आहे.
एकत्रित आणि एकत्रिकरण प्रक्रिया विभेदक समीकरणांचे सोडवण्याचे केंद्र आहेत. तथापि, भेद मध्ये चरणांची विपरीत, एकीकरण मध्ये चरण नेहमी एक स्पष्ट आणि मानक नियमानुसार अनुसरण नाही. कधीकधी आपल्याला असे आढळते की प्राथमिक क्रिया विषयी समाधान स्पष्टपणे व्यक्त करता येत नाही. त्या बाबतीत, विश्लेषणात्मक उपाय सहसा एक अनिश्चित अभिन्न स्वरूपात दिले जाते. कॅल्क्यूलसचे मूलभूत प्रमेय < निश्चित व अनिश्चित असे अभिसरण खालीलप्रमाणे पथ्यकुलतेच्या मूलभूत प्रमेय द्वारा जोडलेले आहेत: एक निश्चित अभिन्न < मोजण्यासाठी, अनिश्चित अभिन्न फंक्शनच्या (तसेच डेरीवेटिव्ह म्हणूनही ओळखले जाते)> शेवटचे बिंदु x = a आणि x = b वर मूल्यांकन करा. एकदा आपण याच कार्यासाठीच्या एकाग्रतेचे मूल्यमापन केल्यावर निश्चित आणि अनिश्चित असंतुलनाचा फरक स्पष्ट होईल.
खालील अभिप्राय विचारात घ्या:
ओके आपण दोघे करू आणि फरक पाहू.
एकात्मतेसाठी, आपण खालील निर्देशांकडे नेत असणाऱ्या निर्देशांकात एक जोडणे आवश्यक आहे:
याक्षणी < सी < आपल्यासाठी फक्त एक स्थिर आहे < C ची नेमकी मूल्य निश्चित करण्यासाठी समस्या मध्ये अतिरिक्त माहितीची आवश्यकता आहे. आपण त्याच्या निश्चित स्वरूपात समान अविभाज्य मूल्यमापन करू. ई., वरच्या आणि खालच्या मर्यादेसह समाविष्ट. ग्राफिक म्हणून बोलणे, आम्ही आता वक्र f (x) = y 3 दरम्यान y = 2 आणि
y = 3 खाली क्षेत्र संगणकीय करत आहोत. >
या मूल्यांकनात पहिली पायरी म्हणजे अनिश्चित अभिन्न मूल्यमापन सारखेच आहे. फरक एवढाच आहे की सध्याच्या काळात आपण सतत < C

जोडू शकत नाही.
या प्रकरणात अभिव्यक्ती खालीलप्रमाणे दिसत आहे:
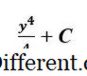
या वळण खालीलप्रमाणे ठरते: मूलत:, आम्ही अभिव्यक्तीमध्ये 3 आणि नंतर 2 बदलले आणि त्यांच्यातील फरक काढला. पूर्वीचे < C वापर करण्याच्या विरूद्ध हे निश्चित मूल्य आहे. काही आणखी तपशीलाने आपण सतत घटक (अनिश्चित इंटीग्रल संदर्भात) शोधूया.
जर फरकाचा

y 3 म्हणजे 3y 2 तर ∫ 3y
2 दि = यु. 3
तथापि,

3y

2
हे अशा बर्याच अभिव्यक्तींचे भिन्नता असू शकते ज्यात काही y 3 < -5, > y
3 +7 , इत्यादी … याचा अर्थ असा होतो की ऑपरेशन दरम्यान निरंतर बेहिशेबी असल्यामुळे उलट परिणाम एकमेव नाही. सर्वसाधारणपणे, 3y 2 हा
y 3 < + सी < वेगळा आहे < सी < कोणताही स्थिरपणा आहे प्रसंगोपात, सींना < 'एकत्रीकरण स्थिर' असे म्हटले जाते. आम्ही हे असे लिहितो: ∫ 3y
2 dx = y 3 + सी एका अनिश्चित अभिन्न साठी एकत्रिकरण तंत्र जसे की टेबल लुकअप किंवा रिस्च इंटिग्रेशन, एकात्मता प्रक्रियेदरम्यान नवीन डिसोन्टिन्युटीज जोडू शकते. हे नवीन खंडित दिसणे कारण अँटी-डेरिव्हेटिव्हज्ला जटिल लॉजिथम जोडणे आवश्यक असू शकते. जेव्हा तर्क चुकीच्या वास्तविक अक्ष ओलांडते तेव्हा कॉम्प्लेक्स लॉगेरिम्सची उडी खंडू होते आणि कधीकधी एकीकरण एल्गोरिदम अशा प्रकारे प्रतिनिधित्व मिळत नाहीत जिथे या जोड्या रद्द होतात.




