समांतरभुज चौकोन आणि समभुज भेदांमधील फरक: समांतरभुज चौकोन

समांतरभुरण बनाम रक्तसंक्रमण समांतरभुज चौकोन आणि समभुज चौकोनाचे तुकडे आहेत या आकड्यांचा भूमिती हजारो वर्षांपासून मनुष्याला ज्ञात आहे. ग्रीक गणितज्ञ युक्लिडने लिहिलेल्या "अॅलेमेंट्स" पुस्तकात हे विषय स्पष्टपणे हाताळले आहे.

समांतरभुज चौकोन समांतरभुज चौकोनाचे चार बाजूंशी भौमितिक आकृती म्हणून परिभाषित केले जाऊ शकते, उलट बाजूस एकमेकांच्या समांतर असतात अधिक तंतोतंत ते समांतर बाजूंच्या दोन जोडीशी एक चतुष्कोण आहे. या समांतर स्वरुपामुळे अनेक भौमितिक वैशिष्ट्ये समांतरलेग्रापासुन मिळतात.

भौगोलिक वैशिष्ट्ये आढळल्यास चौकोनाला एक समांतरभुज आहे.

• विरोध जोडीच्या दोन जोड्या लांबी समान आहेत. (एबी = डीसी, एडी = बीसी) • विरोध करणार्या दोन जोडी आकारमान समान असतात. (

)

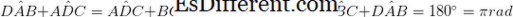• समीप कोन पुरवणी असल्यास • एकमेकांच्या विरोधात असलेल्या बाजूंची एक जोडी समानांतर आणि लांबी समान आहे. (एबी = डीसी आणि AB∥DC)

• कर्ण एकमेकांना दुभागतात (एओ = ओसी, बीओ = ओडी)

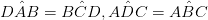
• प्रत्येक कर्ण दोन चतुष्टांश त्रिकोणामध्ये त्रिभुज विभाजित करतो. (ΔADB ≡ ΔBCD, ΔABC ≡ ΔADC)

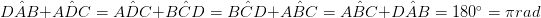
याव्यतिरिक्त, बाजूंच्या चौरसांची बेरीज कर्णांच्या चौरसाकृती समांतर आहे. याला कधीकधी समांतरभुज चौकोन कायदा म्हणून संबोधले जाते आणि भौतिकशास्त्र आणि अभियांत्रिकीमध्ये व्यापक ऍप्लिकेशन्स असतात. (एबी

2

+ BC

2

+ सीडी 2 + डीए ² = एसी ² + बीडी ² ) ^{उपरोक्त सर्व गुणधर्मांचा गुणधर्म म्हणून वापरला जाऊ शकतो, एकदा हे कळले की चौकोनातील एक समांतरभुज चौकोन आहे} समांतरभुज चौकोनचे क्षेत्र एका बाजूच्या लांबीच्या उत्पादनापासून आणि उंचीच्या बाजूस उलट बाजूस मोजले जाऊ शकते. म्हणून, समांतरभुज चौकोनचे क्षेत्र ^{समांतरभुज चौकोनचे क्षेत्रफळ = उंची = एबी × एच समांतरभुज चौकोनचे क्षेत्र स्वतंत्र समांतरभुज चौकोनच्या आकारापेक्षा वेगळे आहे. हे केवळ बेस आणि लांबीच्या उंचीवर अवलंबून असते.} समांतरभुज चौकोनाच्या बाजूस दोन वेक्टर्स दर्शवल्या जाऊ शकतात, तर क्षेत्र दोन समीप सदिशांच्या वेक्टर उत्पादनाच्या (क्रॉस उत्पादन) विशालतेने मिळू शकते. ^{जर बाजू AB आणि AD यांना क्रमशः वेक्टर्स () आणि () प्रस्तुत केले असल्यास, समांतरभुजांचा प्रदेश} ने दिलेला आहे, जेथे α हा

आणि दरम्यानचा कोन आहे >

समांतरभुज चौकोनचे काही प्रगत गुणधर्म खालील आहेत;

• समांतरभुज चौकोनचे क्षेत्र कोणत्याही त्रिकोणाच्या दोन त्रिकोणाचे क्षेत्र दुप्पट आहे.

• समांतरभुज चौकोनचे क्षेत्रफळ मध्यबिंदूतून जाणार्या कोणत्याही ओळीद्वारे अर्ध्या भागात विभागले आहे.

• कोणत्याही अपरिपक्व आनुवंशिक परिवर्तन दुसर्या समांतरभुज चौकोन समांतरभुज चौकोन घेते. • समांतरभुज चौकोन ऑर्डर 2 = 99 9 च्या घमेंळी सममिती आहे • बाजूंच्या समांतरभुज चौकोनमधील अंतराच्या कोणत्याही बिंदूंपासून स्वतंत्र आहे पॉइंटचा स्थान

समभुज सर्व बाजूंविना चतुर्भुज समान लांबीच्या समभुजांची एक समभुज म्हणून ओळखली जाते. त्याला

समभुज चौकोन असे नाव दिले आहे खेळणा-या कार्डेसारख्याच हिराचे आकार मानले जाते.

समांतरभुज चौकोनचे एक विशिष्ट रूप Rhombus देखील आहे. हे सर्व चार बाजूंना समान समांतरभुज चौकोन मानले जाऊ शकते. समांतरभुज चौकोनच्या गुणधर्मांव्यतिरिक्त त्याच्याकडे विशेष गुणधर्म आहेत.

• समभुज चौकोनाचे दुहेरी कोन एकमेकांना विखुरतात; कर्ण लंब आहेत.

• कर्ण दोन विरुद्ध आंतरकेंद्रांची दुभागणी करतात.

• संलग्न पक्षांपैकी किमान दोन लांबी समान आहेत.

समभुज चौकोन सारख्याच पद्धतीने समभुज चौकोन काढले जाऊ शकते.

समांतरलाग्राहोग आणि समभुज यांचा काय फरक आहे?

• समांतरभुज चौकोन आणि समभुज चौकोन हे चौकोनी तुकडे असतात. समभुज चौकोन एक विशेष केस आहे. • कोणत्याही क्षेत्राचे सूत्र बेस × उंचीचा वापर करून गणले जाऊ शकते. • कर्ण विचार करणे;

- समांतरभुज चौकोनचे कर्ण एकमेकांना दुभागतात आणि समांतरभुज त्रिकोण दोन समकक्ष त्रिकोण तयार करतात.

- समभुज चौकोनाचे दुहेरी कोन एकमेकांना दुभंगले आणि त्रिकोण तयार समभुज आहेत.

• अंतर्गत कोन लक्षात घेता; - समांतरभुज चौकोनचे आंतरकोनिक आकृतीचे आकार समान असतात. दोन संलग्न आंतरिक कोन पूरक आहेत.

- समभुज त्रिकोणाचे आतील कोन दुभंगून विस्कळित आहेत. • बाजूंचा विचार करणे; - समांतरभुज चौकटीत, बाजूंच्या चौरसांची बेरीज कर्णकाच्या (समांतरभाषा) चौकांच्या बेरजेइतकी असते.

- सर्व चार बाजू समभुज चौकोनात असाव्यात म्हणून, एका बाजूला चौरस वेळा चौकोनाचे माप त्या कर्णकाच्या वर्गांच्या बेरजेएवढे असते.