तार्किक आणि असमंजसपणाचे आकडे दरम्यान फरक
"संख्या" हा शब्द आपल्या मनात आणला जातो जे साधारणपणे शून्य पेक्षा अधिक सकारात्मक पूर्णांक मूल्यांप्रमाणे वर्गीकृत करतात. इतर वर्गांच्या संख्येत संपूर्ण संख्या आणि अपभणांक <, जटिल आणि वास्तविक संख्या < आणि नकारात्मक पूर्णांक मूल्यांचे < असे आहेत. संख्येचे वर्गीकरण अधिक पुढे वाढवून, आम्हाला तर्कसंगत < आणि अपरिपक्व < क्रमांक आढळतात. एका कारणाचा क्रमांक म्हणजे एक अपूर्णांक. दुसर्या शब्दात, तर्कसंगत संख्या दोन संख्यांचा अनुपात म्हणून लिहीली जाऊ शकते.
उदाहरणार्थ, संख्या 6 वर जरा विचार करा. हे दोन संख्यांचा अनुपात म्हणून लिहीले जाऊ शकते उदा. 6
आणि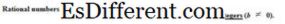
1 , ज्यामुळे गुणोत्तर असेल < 6/1 . त्याचप्रमाणे, 2/3 , जे अपूर्णांक म्हणून लिहिलेले आहे, हे तर्कशुद्ध संख्या आहे. अशा प्रकारे, आपण तर्कशुद्ध संख्या परिभाषित करू शकता, जसे की एका अपूर्णांकाच्या स्वरूपात लिहिलेल्या संख्येप्रमाणे, ज्यामध्ये दोन्ही अंशात (सर्वात वरची संख्या) आणि भाजक (खाली असलेली संख्या) पूर्ण संख्या आहेत. व्याख्या म्हणून, प्रत्येक संपूर्ण संख्या देखील एक सुसंगत संख्या आहे.
उलट, कोणतीही संख्या जी अपूर्णांक किंवा गुणोत्तर स्वरूपात व्यक्त केली जाऊ शकत नाही तिला अपवरमेय म्हणतात. एक असमंजसपणाचे क्रमांक
√2 (< 1 414213 …) < याचे सर्वात सामान्यपणे उल्लेखित उदाहरण. असमंजसपणाचे एक दुसरे उदाहरण म्हणजे संख्यात्मक स्थिरांक π ( 3 141592 … ) .
चौरस संख्यांच्या केवळ वर्गमांचा; मी. ई., परिपूर्ण चौरसांची वर्गमूळे < तर्कसंगत आहेत.
√2 (असमंजसपणाचे) √3 (असमंजसपणाचे) √4 < = 2 (तर्कसंगत) √5, √6, √7, 88 (अपरिहार्य) 9 9 99 = 3 (तर्कसंगत) आणि असेच काही. पुढे, आम्ही लक्षात ठेवा की, केवळ
n व्या मुळे n
व्या सामर्थ्य तर्कसंगत आहेत.64 हा एक 6 व्या < शक्ती आहे, म्हणजे < 6 व्या < अशा प्रकारे < 6 व्या
< 2 < ची शक्ती पण 6 व्या
root ची 63
असमंजसपणाचे आहे 63 एक परिपूर्ण नाही
6 व्या
शक्ती
जेव्हा आपण दशांश म्हणून तर्कसंगत क्रमांक व्यक्त करतो, तेव्हा दशांश अचूक < ( 1/5 = 0 प्रमाणे 20) किंवा हे अयोग्य < होईल (जसे, 1/3 ≈ 03333 ). दोन्हीपैकी कुठल्याही बाबतीत, अंकांचा अपेक्षित नमुना असेल. लक्षात घ्या की जेव्हा एक असमंजसपणाचे < संख्या दशांश म्हणून व्यक्त केली जाते, तेव्हा स्पष्टपणे ते अयोग्य होईल, कारण अन्यथा, तर्कसंगत होईल. शिवाय, अंकांचा अपेक्षित नमुना दिसणार नाही. उदाहरणार्थ, √2 ≈ 1 4142135623730950488016887242097 आता, तर्कशुद्ध संख्येसह, आम्ही कधीकधी 1/11 = 0. 0 9 090 9 < समोर येतो. दोन्ही समान चिन्हाचा वापर ( = ) आणि तीन बिंदू ( ellipsis ) असे दर्शवतात की तरीही 1/11 हे व्यक्त करणे शक्य नाही दशांश म्हणून, आपण तरीही 1/11
जवळ मिळविण्यासाठी परवानगी म्हणून अनेक दशांश अंकांसह ते अंदाजे करू शकता.अशाप्रकारे, < 1/11
चे दशांश स्वरूप असंभव समजलं जातं. त्याच टोकनद्वारे, ¼ चे दशांश स्वरूप जे 25 आहे, बरोबर आहे. असमंजसपणाचे आकडेमोडीसाठी दशमलव स्वरूपाकडे येणे, ते नेहमी अयोग्य ठरणार आहेत. √ 2 चे उदाहरण पुढे चालू ठेवल्यावर, आम्ही √2 = 1 41421356237 … (एलीपिसिसचा वापर लक्षात घ्या) लिहितो तेव्हा लगेच सूचित होते की > √2 अचूक असेल. पुढे, अंकांचा अंदाज पटल असणार नाही. संख्यात्मक पद्धतींमधील संकल्पना वापरणे, पुन्हा एकदा, आपण तर्कशुद्धपणे अंदाजे किती दशांश आकडय़ांपर्यत जाऊ शकतो जोपर्यंत आपण √2 जवळ असतो. तर्कसंगत आणि असमंजसपणाचे आकडे वर कोणतीही टीप अनिवार्य पुराव्याशिवाय समाप्त करू शकत नाही कारण √2 असमंजसपणाचे आहे का असे करताना, आम्ही एक स्पष्ट उदाहरण देतो, प्रति < परिशीलता द्वारे पुरावा. समजा √2 हे तर्कसंगत आहे. हे आपल्याला दोन पूर्णांकांचे गुणोत्तर म्हणून त्याचे प्रतिनिधित्व करण्यास प्रवृत्त करते, असे म्हणतात की
p < आणि
q
√2 = p / q हे सांगणे अनावश्यक, p
आणि q सर्वसामान्य घटक नाहीत, कारण जर कोणतेही सामान्य घटक असतील तर आम्ही ते रद्द केले असते अंश आणि भाजक पासून त्यांना बाहेर. समीकरणाच्या दोन्ही बाजुंची समोरासमोर, आपण शेवट करतो,
हे म्हणून सोयीस्कर पद्धतीने लिहीले जाऊ शकते, p 2 = 2q > 2 शेवटचा समीकरण सुचवितो की
p 2 तो अगदी आहे हे केवळ तेंव्हा शक्य आहे जेव्हा p स्वतःच अगदी आहे. यामधून असे सूचित होते की p 2 हे <3 4 द्वारे विभाज्य आहे. म्हणून, q
2 आणि म्हणूनच q
अगदीच असणे आवश्यक आहे.मगp आणि q दोन्हीही आपल्या सुरुवातीच्या धारणास एक विरोधाभास आहे जे त्यांच्याकडे सामान्य घटक नाहीत. अशाप्रकारे, < √2 तर्कसंगत असू शकत नाही. प्र. ई डी डी. <


