फ्रिक्वेंसी आणि सापेक्ष वारंवारतेमध्ये फरक
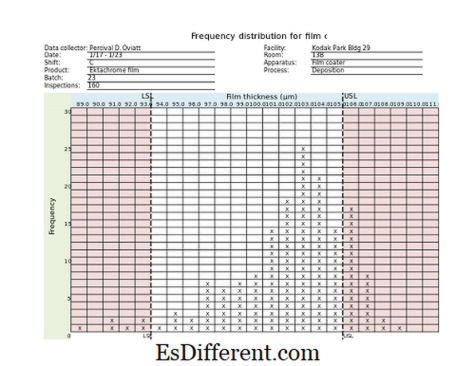
वारंवारिता वि संबंधित वारंवारता
आकडेवारी किंवा गणित मध्ये संभाव्यता बद्दल चर्चा "अटी वारंवारता" आणि "सापेक्ष वारंवारता" सहसा अप चालू. संभाव्यता एक असा विश्वास व्यक्त करते की विशिष्ट परिणाम प्रयोग, चाचणी किंवा संशोधनात होईल; तो एक विशिष्ट कार्यक्रम होण्याची शक्यता निश्चित करण्यासाठी वापरला जातो. इव्हेंटची संभाव्यता काही प्रयोग करून आणि काही किरकोळ गणना केल्याने निर्धारित केले जाऊ शकते. बहुतेक लोक आकडेवारीत संभाव्यता वापरतात; काही जण अभ्यास, अभ्यास, गणित, विज्ञान, अर्थ किंवा अगदी जुगार यासारख्या इतर विषयांमध्ये त्याचा वापर करतात.
आकडेवारी मध्ये, वारंवारता एक प्रयोग किंवा अभ्यासात दिलेल्या परिणामी वेळेची एकूण संख्या आहे; इव्हेंटची एकूण संख्या येते. असे म्हटले जाऊ शकते की वारंवारतेचा प्रत्यय केवळ याचाच अर्थ आहे. उदाहरणार्थ, आपण फाटा फेकताना सहा मिळण्याची संभाव्यता निश्चित करण्यासाठी एक चाचणी कार्यान्वित करणार आहात. आपण फासे दहा वेळा फेकून घ्या, आणि त्यावरील सहा डॉट्स असलेल्या डाइसची बाजू तीन वेळा दाखविली. परिणाम "तीन वेळा" आपली वारंवारिता आहे. पत्त्याच्या डेकमधून कार्ड काढणे संभाव्यतेची चाचणी घेण्याचे आणि हृदय वारंवारता मिळविण्याचे आणखी एक मार्ग आहे ज्यामध्ये हृदय काढले जाईल. पाच कार्डे निवडा आणि पहा की त्यावर त्यांचे हृदय चिन्ह किती आहेत. समजा तुम्हाला तीन हृदय कार्डे मिळाली - ही तुमची वारंवारता आहे. गणना करणे आवश्यक न झाल्यास आपण प्रयोग केल्यानंतर आपण वारंवार वारंवार प्राप्त करू शकता.

दुसरीकडे, "सापेक्ष वारंवारता" हा शब्द एकूण प्रयत्नांच्या संख्येपेक्षा किती वेळा होतो याचा काही भाग वापरला जातो. वारंवारतेच्या विपरीत, ज्यायोगे तुम्ही प्रयोग करून सहजपणे येऊ शकता, सापेक्ष वारंवारता मध्ये काही सोप्या आकडेमोडींचा समावेश असतो. आम्हाला असे गृहीत धरूयात की आपण एक नाणे टाकून, एक कार्ड काढता, एक फाटा फोडून किंवा दगडांमधून बाहेर काढत, आणि नंतर "एन" वेळा या कृत्याची पुनरावृत्ती करून एक अनन्य प्रयोग करीत आहात. नंतर, आपण निश्चित कालावधीची पूर्ण वारंवारता लक्षात घेता. सापेक्ष वारंवारता प्राप्त करण्यासाठी वापरलेला सूत्र अत्यंत सोपी आहे; प्रयोगाचा पुनरावृत्ती होण्याच्या एकूण संख्येच्या तुलनेत सापेक्ष वारंवारता जितकी वेळा असते तितकी असते.
उदाहरणार्थ, आपण एका पिशव्यातून रंगीत बॉल ड्रॉ करून यादृच्छिक प्रयोग करीत आहात. आपण दहा चेंडू पिशव्यामधून बाहेर काढू शकता, आणि तुम्ही बघू शकता की लाल चेंडूत पाच वेळा आले. या प्रकरणात, सापेक्ष वारंवारता दशांश 5/10 किंवा ½ - 0. 5 आहे. दुसरे चांगले उदाहरण म्हणजे ते संगणक मॉनिटरच्या उत्पादनातून नमुन्यांना घेऊन ते योग्यरित्या कार्य करीत आहे किंवा नाही हे पाहण्यासाठी. आम्ही दोषपूर्ण विषयांची सापेक्ष वारंवारता तपासण्यासाठी आणि ते निश्चित करण्यासाठी संगणक मॉनिटरचे 50 यादृच्छिक नमुने घेतो.प्रयोग आयोजित करताना, आम्ही शिकलो की दहा संगणक मॉनिटर्स दोषपूर्ण असतात. पुन्हा आम्ही परीक्षण केलेल्या नमुन्यांची संख्या प्रती दोषपूर्ण संगणक मॉनिटर्स विभाजित करून सापेक्ष वारंवारता प्राप्त; चाचणी केलेल्या 50 संगणक मॉनिटर्सद्वारे विभाजित केलेले 10 दोषपूर्ण संगणक मॉनिटर. आपल्याला 10/50 किंवा 1/5 मिळतात जे 0. आहे. 2. सारांश:
1. वारंवारता हा परिणाम म्हणजे किती वेळा येतो, तर "सापेक्ष वारंवारता" हा परिणाम म्हणजे किती वेळा प्रयोग पुन्हा केला जातो त्या संख्येने विभागलेला असतो.
2 वारंवारता सहजपणे एक साधी प्रयोग आयोजित करून आणि प्रश्नातील इव्हेंटमध्ये किती वेळा येते हे निर्धारीत केले जाऊ शकते; नाही गणिताची आवश्यकता आहे दुसरीकडे, सोपी डिव्हिजन वापरून सापेक्ष वारंवारता निर्धारित केली जाते. <




