समांतरभुज चौकोन आणि चतुर्भुज दरम्यान फरक: समांतरभुज चौकोन चतुर्भुज
समांतरलाग्राम बनाम चतुर्भुज क्वाड्रिलाटार्लेल्स आणि पॅरललोग्राम हे युक्लिडियन भूमितीमध्ये आढळणारे बहुभुज आहेत. समांतरभुज चौकोनचे विशेष प्रकार आहे. क्वाड्रिलेटलल्स प्लॅनर (2 डी) किंवा 3 डायमेन्शनल असू शकतात आणि पॅरेरलअॅग्राम नेहमीच तारे असतात.
चतुर्भुज चतुष्कोण चार बाजूंनी बहुभुज आहे. यात चार शिरोबिंदू आहेत आणि त्यातील अंतर्गत कोनांची बेरीज 3600 (2π rad) आहे. क्वाड्रिलेटलल्स हे स्व-छेदने व साध्या चतुर्थी श्रेणींमध्ये वर्गीकृत आहेत. स्वत: ची छेदणारे चौकोनी तुकडे दोन किंवा दोन बाजू एकमेकांना ओलांडत आहेत, आणि लहान भौमितिक आकृत्या (जसे की त्रिभुज चौकोनमध्ये तयार होतात).
साध्या चतुर्भुजांना देखील बहिर्वक्र आणि अंतर्गोल चौगुरी विभागात विभागले आहे. अंतराचे चौकोनी तुकडेजवळ असलेल्या बाजूंनी पृष्ठभागावर रिफ्लेक्स कोन बनविणे. साधारण चौकोनी तुकडे ज्यात आंतरिकरित्या रिफ्लेक्स कोन नसतात त्या बहिर्गोल चौकोन आहेत. बहिर्वक्र चौकोनी अवयवांमध्ये नेहमी tessellations असू शकतात.

प्रारंभिक पातळीवरील चतुर्भुज रचनेतील भूमितीचा एक मुख्य भाग बहिर्गोल चौकोन काही चतुर्भुजल आपल्याला प्राथमिक शाळांच्या दिवसांपासून खूप परिचित आहेत. खालील बहिर्गोल चौकोनी तुकडे दर्शविणारे आकृती आहे.

समांतरभुज चौकोन समांतरभुज चौकोनाचे चार बाजूंशी भौमितिक आकृती म्हणून परिभाषित केले जाऊ शकते, उलट बाजूस एकमेकांच्या समांतर असतात अधिक तंतोतंत ते समांतर बाजूंच्या दोन जोडीशी एक चतुष्कोण आहे. या समांतर स्वरुपामुळे अनेक भौमितिक वैशिष्ट्ये समांतरलेग्रापासुन मिळतात.
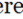
• विरोध जोडीच्या दोन जोड्या लांबी समान आहेत. (एबी = डीसी, एडी = बीसी) • विरोध करणार्या दोन जोडी आकारमान समान असतात. ()

• समीप कोन पुरवणी असल्यास • एकमेकांच्या विरोधात असलेले दुहेरी बाजू समानांतर आणि लांबी समान आहे. (एबी = डीसी आणि एबीसीडीसी)
• कर्ण एकमेकांना दुभागतात (एओ = ओसी, बीओ = ओडी)
• प्रत्येक कर्ण दोन चतु: त्रिकोण त्रिकोणामध्ये विभाजित करतो. (ΔADB ≡ ΔBCD, ΔABC ≡ ΔADC)

समांतरभुज चौकोन कायदा म्हणून संबोधले जाते आणि भौतिकशास्त्र आणि अभियांत्रिकीमध्ये व्यापक ऍप्लिकेशन्स असतात. (एबी
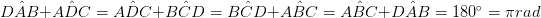
2
+ BC
2
+ सीडी 2 + डीए 2 = एसी 2 + बीडी 2 ) उपरोक्त सर्व गुणधर्मांचा गुणधर्म म्हणून वापरला जाऊ शकतो, एकदा हे कळले की चौकोनातील एक समांतरभुज चौकोन आहे समांतरभुज चौकोनचे क्षेत्र एका बाजूच्या लांबीच्या उत्पादनापासून आणि उंचीच्या बाजूस उलट बाजूस मोजले जाऊ शकते. म्हणून, समांतरभुज चौकोनचे क्षेत्र समांतरभुज चौकोनचे क्षेत्रफळ = उंची = AB × h
समांतरभुज चौकोनाचे क्षेत्र स्वतंत्र समांतरभुज चौकोनच्या आकारापासून स्वतंत्र आहे. हे केवळ बेस आणि लांबीच्या उंचीवर अवलंबून असते.
समांतरभुज चौकोनाच्या बाजूस दोन वेक्टर्स दर्शवल्या जाऊ शकतात, तर क्षेत्र दोन समीप सदिशांच्या वेक्टर उत्पादनाच्या (क्रॉस उत्पादन) विशालतेने मिळू शकते.
जर बाजू AB आणि AD यांना क्रमशः वेक्टर्स () आणि () प्रस्तुत केले असल्यास, समांतरभुजांचा प्रदेश ने दिलेला आहे, जेथे α हा आणि दरम्यानचा कोन आहे > समांतरभुज चौकोनचे काही प्रगत गुणधर्म खालील आहेत;

• समांतरभुज चौकोनचे क्षेत्र कोणत्याही त्रिकोणाच्या दोन त्रिकोणाचे क्षेत्र दुप्पट आहे.
• समांतरभुज चौकोनचे क्षेत्रफळ मध्यबिंदूतून जाणार्या कोणत्याही ओळीद्वारे अर्ध्या भागात विभागले आहे.
• कोणत्याही अपरिपक्व आनुवंशिक परिवर्तन दुसर्या समांतरभुज चौकोन समांतरभुज चौकोन घेते. • समांतरभुज चौकोन ऑर्डर 2 = 99 9 च्या घमेंळी सममिती आहे • बाजूंच्या समांतरभुज चौकोनमधील अंतराच्या कोणत्याही बिंदूंपासून स्वतंत्र आहे बिंदूचे स्थान





• कोणतीही कर्ण दोन समान त्रिकोणांत समांतरभुज चौकोन करतो, तर सामान्य चौकोनच्या कर्णकाद्वारे तयार केलेले त्रिकोण हे एकरुप नसतात.



